自从deep learning成为研究热点之后,为了解决不同种类的问题,神经网络的结构愈发复杂起来,面对图像信息的提取与图像特征的学习,CNN已经成为众多神经网络的佼佼者,由于CNN与普通网络的区别,训练的BP算法也需要进行相应的调整,为此笔者查阅了一些资料,现将CNN的BP算法整理如下:
Features of CNN
Convolution layer
卷积层引入了卷积核的概念,输出向量可以理解为是卷积核与输入向量卷积产生的结果,因此并不是全连接的关系,在这里我们可以回忆一下卷积运算的定义:卷积是通过两个函数f和g生成另一个函数的计算方法,其计算公式为:
\[(f*g)[n] = \sum_{m=-\infty}^\infty f[n-m] \times g[m]\]
直观一点就是将函数f绕y轴翻转从左向右平移,计算f与g的重叠部分的面积,如下图(Wiki)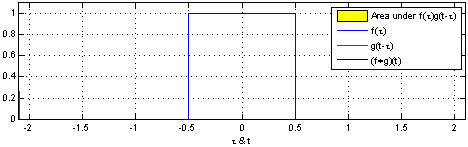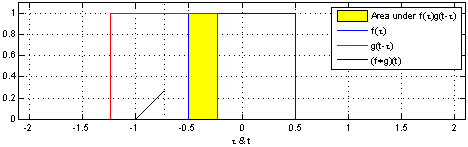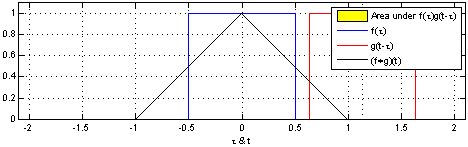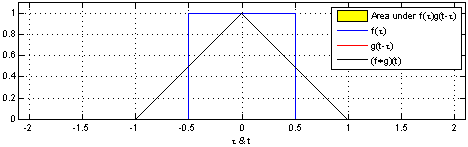
因此在CNN的卷积运算中,我们可以认为将卷积核翻转后在原始图像上进行滑动,计算重叠部分的elementwise的乘积并求和,用数学公式表达就是: \[x_j^l = f(\sum_{i \in M_j} x_i^{l-1} * k_{ij}^l + b_j^l)\]
式中j表示第j个feature map,l表示第l层,\(M_j\)表示原图像与卷积和的重叠部分,在这里仅仅因为完整性才加上j,为了理解卷积层的反向传播,我们假设feature map只有一个,即卷积核的数量为1
Pooling layer
池化层比卷积层来得简单,无论是MaxPooling还是Average Pooling我们很容易找到输入与输出向量的关系,需要注意的是对于MaxPooling,计算最大值的同时需要记住该最大值的下标,因为在反向传播时需要用到该下标。
BackPropagation
按照BP算法的流程, 我们只要知道这一节中我们假设BP算法已经反向传播到最后一个全连接层,记为\(\delta^l\)
Pooling layer
先从比较简单的池化层入手,注意到输入向量在经过池化层之后,假设原始图像尺寸为\(H\*W\), 窗口尺寸为d,且窗口滑动不重叠,则输出向量的尺寸为: \[H*W -> Ceil(H/d) * Ceil(W/d)\]
由于Pooling层没有权值矩阵参与运算,仅仅是压缩了原始向量的尺寸,因此在进行反向传播时,也只需要将残差delta“放大”到原来的大小就可以了,pooling的数学表达式及其偏导关系为:
\[g(x)= \begin{cases}\sum_{k=1}^mx_k \over m, \ & {\partial g \over \partial x} = {1 \over m } \ mean \ pooling \cr max(x) & {\partial g \over \partial x} = {\begin{cases} 1 &if \ x_j = max(x) \cr 0 &otherwise \ max \ pooling \end{cases}} \end{cases}\]
pooling的BP算法,看上去复杂其实原理非常简单,我们只需要进行一步上采样upsampling的操作:
- maxpooling:将输出向量的每个元素扩展成d*d的矩阵,前向传播时记录的下标所对应的元素为该元素的值,其他置为0
- meanpooling:只需要将矩阵中元素都置为该元素的值就可以了
我们把上采样记作\(up(x)\),因此残差在经过pooling层时,可以简单地计算上一层残差为
\[\delta^{l} = f^{'}(u_j^l \circ up(\delta_j^{l+1}))\]
式中\(f\)表示pooling层后接的激活函数,\(u\)表示该\(f\)的输入,但是很多的CNN架构中Pooling层中这一项为1,\(\circ\)指elementwise乘法
Convolution layer
其实在卷积层我们也用到了池化压缩的思想,但是卷积层有卷积核,相当于全连接层的权值矩阵,因此我们可以类比fc层的残差计算方法:
\[\delta^{l-1} = (W^T \delta^{l}) * f^{'}(u^{l-1})\]
卷积层不像全连接层那样输入与输出之间每两个元素都有联系,前向传播时对于输出向量中的每个元素,在输入向量中与之相关联的元素只有d*d个,即卷积窗口的大小,我们很容易通过下图看出对应关系: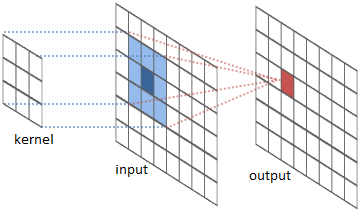
因此反向传播时,我们也只需要考虑部分的对应关系,为了简单我们以一维向量的卷积为例: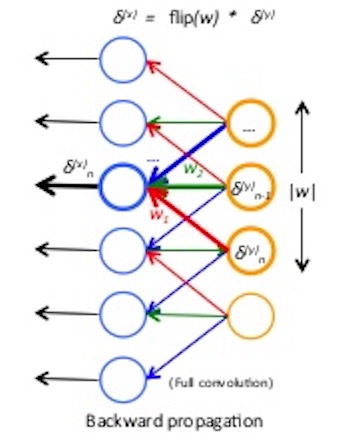
\[\delta_n^{l-1} = {\partial J \over \partial x_n} = {\partial J \over \partial y}{\partial y \over \partial x_n} = \sum_{i=1}^{|w|} {\partial J \over \partial y_{n-i+1}}{\partial y_{n-i+1} \over {\partial x_n}} = \sum_{i=1}^{|w|} {\delta_{n-i+1}^{l}w_i} = (\delta^{l}*flip(w))[n]\]
式中w代表卷积核的参数,上式的结果可以简化为:
\[\delta^{l-1} = \delta^{l} * flip(w)\] 这里我们忽略了激活函数\(f\),可以看出该公式与全连接层的公式十分类似,式中flip表示翻转,意思是在反向传播时需要将卷积核进行翻转
这里其实有一个trick,在标准的卷积运算中定义了翻转因此在反向传播时我们也对应进行翻转,但是在实际训练时我们不进行翻转的话,在BP过程中就不需要翻转回来 事实上,由于卷积层训练的就是卷积核的参数,因此我们不翻转同样可以训练,而且可以简化计算过程
残差的反向传播已经完成,下面就是通过残差计算偏导了,全连接层在计算偏导时只需要将后一层的残差向量乘以前面一层的对应元素即可,但是卷积核的滑动窗口特性,实际参与计算的元素要多一些,所以我们需要修改一下:
\[{\partial J \over \partial {k_{ij}^{l}}} = \sum_{u,v} ({\delta_{j}^{l}}_{uv}(p_{i}^{l-1})_{uv})\]
式中p表示的是原输入向量中与卷积核元素\(k_{ij}\)相乘的元素,如下图所示: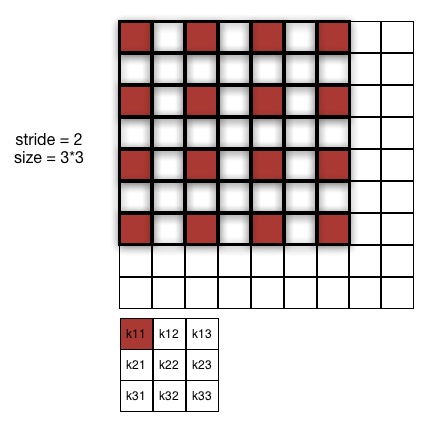
假设步长为2,那么\(p_i\)指的就是图中红色的部分,如果步长设置为1,那么\(p_i\)指的就是图像中阴影加粗的部分
Conclusion
经过分析我们可以得出CNN的反向传播其实也有规律可循,关键是需要了解BP算法的原理,这是理清任何使用BP算法进行优化求解的神经网络的基本,抓住两个点:反向传播其实是将输出层作为输入层计算各层残差的过程,把握好各层的性质理解起来就比较容易了。
Reference
Bouvrie J. Notes on convolutional neural networks[J]. 2006.
http://www.slideshare.net/kuwajima/cnnbp